Cryptography#
Why cryptography?
Cryptographic analysis provides distinct advantages over some more en vogue comp neuro methods, like deep learning
It sits at a crucial point between supervised and unsupervised learning: you don’t need training labels, but you also pull on pre-existing knowledge about the structure of information in the world
Cryptographic analysis centers on using the underlying non-uniform distribution of data in the world to decode information
This is something humans naturally do to learn – e.g. children use morpheme co-ocurance-rates to learn language
On a similar note, human adults are able to remember larger numbers of social relationships when they exhibit properties that make them representable in a lower number of bits
What will we cover in this notebook?
A hands-on example of using cryptographic analysis to break a substitution cipher in English
Run the cell below to download data and prepare our environment!#
#file imports
import nltk
from nltk.corpus import words as wordlist
import re
import pandas
from collections import Counter
import matplotlib.pyplot as plt
import numpy as np
import random
import os
from IPython.display import HTML, display
import string
#set random seed and download corpora
os.environ['PYTHONHASHSEED'] = '0'
nltk.download('words')
nltk.download('gutenberg')
#make sure the display fits the width of the page
def set_css():
display(HTML('''
<style>
pre {
white-space: pre-wrap;
}
</style>
'''))
get_ipython().events.register('pre_run_cell', set_css)
def get_letter_distribution(text, plot=False, title='', zipfian=False):
text = re.sub(r'[^a-z]', '', text.lower())
letter_counts = Counter(sorted(text))
if plot:
if zipfian:
letters, vals = zip(*letter_counts.most_common())
letters = np.array(letters)
vals = np.array(vals).astype('float64')
vals /= sum(vals)
plt.bar(letters, vals)
else:
plt.bar(letter_counts.keys(), np.array(list(letter_counts.values()))/len(text))
plt.ylim([0,0.2])
plt.xlabel('letter')
plt.ylabel('percentage of all letters')
plt.title(title)
plt.show()
return letter_counts
alphabet = list(string.ascii_lowercase)
random.shuffle(alphabet)
cipher = dict(zip(sorted(alphabet), alphabet))
for letter in alphabet:
cipher[letter.upper()] = cipher[letter].upper()
original_quote = nltk.corpus.gutenberg.raw(nltk.corpus.gutenberg.fileids()[1])
encrypted_quote = ''
for letter in original_quote:
if letter in cipher.keys():
encrypted_quote+=(cipher[letter])
else:
encrypted_quote+=(letter)
def decrypt(encrypted_quote, reverse_cipher):
unencrypted_quote = ''
for letter in encrypted_quote:
if letter in reverse_cipher.keys():
unencrypted_quote+=(reverse_cipher[letter])
else:
unencrypted_quote+=(letter)
return unencrypted_quote
def fix_single_letter_words(encrypted_quote, reverse_cipher):
single_letter_words = []
for word in re.sub(r'[^a-zA-Z ]', '', encrypted_quote.lower()).split():
if len(word) == 1:
single_letter_words.append(word)
(first, count1), (second, count2) = Counter(single_letter_words).most_common()[0:2]
if reverse_cipher[first] != 'a':
for letter in reverse_cipher.keys():
if reverse_cipher[letter] == 'a':
reverse_cipher[letter] = reverse_cipher[first]
if reverse_cipher[letter] == 'A':
reverse_cipher[letter] = reverse_cipher[first].upper()
reverse_cipher[first] = 'a'
reverse_cipher[first.upper()] = 'A'
if reverse_cipher[second] != 'i':
for letter in reverse_cipher.keys():
if reverse_cipher[letter] == 'i':
reverse_cipher[letter] = reverse_cipher[second]
if reverse_cipher[letter] == 'I':
reverse_cipher[letter] = reverse_cipher[second].upper()
reverse_cipher[second] = 'i'
reverse_cipher[second.upper()] = 'I'
return reverse_cipher
english = set(wordlist.words())
def get_percent_real(recovered):
english = set(wordlist.words())
reals = [word in english for word in re.sub(r'[^a-zA-Z ]', '', recovered.lower()).split()]
percent_real = sum(reals)/len(reals)
return percent_real
import copy
def swap_keys(reverse_cipher, L1, L2):
updated = copy.deepcopy(reverse_cipher)
L1V, L2V = reverse_cipher[L1], reverse_cipher[L2]
updated[L1], updated[L2] = L2V, L1V
updated[L1.upper()], updated[L2.upper()] = L2V.upper(), L1V.upper()
return updated
def swap_keys_inplace(reverse_cipher, L1, L2):
L1V, L2V = reverse_cipher[L1], reverse_cipher[L2]
reverse_cipher[L1], reverse_cipher[L2] = L2V, L1V
reverse_cipher[L1.upper()], reverse_cipher[L2.upper()] = L2V.upper(), L1V.upper()
def improve_deciphering(second_pass, reverse_cipher, percent_real_before):
english = set(wordlist.words())
c = get_letter_distribution(second_pass)
dists = np.ones((26,26))
for i in range(26):
for j in range(i+1,26):
dists[i,j] = abs(c[alphabet[i]] - c[alphabet[j]])/sum(c.values())
percent_real = percent_real_before
indeces = np.argsort(dists.flatten())
while percent_real < 0.81:
for idx in indeces:
i,j=np.unravel_index(idx, (26,26))
L1, L2 = alphabet[i], alphabet[j]
updated = swap_keys(reverse_cipher, L1, L2)
unencrypted_quote = ''
for letter in encrypted_quote:
if letter in updated.keys():
unencrypted_quote+=(updated[letter])
else:
unencrypted_quote+=(letter)
reals = [word in english for word in re.sub(r'[^a-zA-Z ]', '', unencrypted_quote.lower()).split()]
percent_real = sum(reals)/len(reals)
print(percent_real)
if percent_real > percent_real_before+(0.82-percent_real_before)/4:
print(percent_real, '\t', L1, '\t',L2,'\n\n')
print(re.sub(r'[^a-zA-Z ]', '', unencrypted_quote.lower())[35:776])
swap_keys_inplace(reverse_cipher, L1, L2)
percent_real_before = percent_real
break
return reverse_cipher
[nltk_data] Downloading package words to /home/runner/nltk_data...
[nltk_data] Unzipping corpora/words.zip.
[nltk_data] Downloading package gutenberg to /home/runner/nltk_data...
[nltk_data] Unzipping corpora/gutenberg.zip.
Let’s use some cryptanalysis to solve a letter subtitution cipher. The text below is a passage from a classic novel in which each letter has been replaced with another letter from the English alphabet, with unique pairings.
print(encrypted_quote[35:776])
Ijvtdxl 1
Mul Nvgdxl Xgguwd, wh Qxggzoij Jvgg, uo Mwaxlmxdmjulx, nvm v avo njw,
hwl jum wno vafmxaxod, oxcxl dwwq ft voz rwwq rfd djx Rvlwoxdvyx;
djxlx jx hwfob wiiftvduwo hwl vo ubgx jwfl, vob iwomwgvduwo uo v
bumdlxmmxb wox; djxlx jum hvifgduxm nxlx lwfmxb uodw vbaulvduwo vob
lxmtxid, rz iwodxatgvduoy djx guaudxb lxaovod wh djx xvlguxmd tvdxodm;
djxlx voz fonxgiwax mxomvduwom, vlumuoy hlwa bwaxmdui vhhvulm
ijvoyxb ovdflvggz uodw tudz vob iwodxatd vm jx dfloxb wcxl
djx vgawmd xobgxmm ilxvduwom wh djx gvmd ixodflz; vob djxlx,
uh xcxlz wdjxl gxvh nxlx twnxlgxmm, jx iwfgb lxvb jum wno jumdwlz
nudj vo uodxlxmd njuij oxcxl hvugxb. Djum nvm djx tvyx vd njuij
djx hvcwfludx cwgfax vgnvzm wtxoxb:
"XGGUWD WH QXGGZOIJ JVGG.
"
If we wanted to decrypt this, we could try a few approaches. We could brute force it, trying every single possible combination of unique letter replacement pairs. This comes out to \(26! = 4.03e^{26}\) potential combinations, which would take a prohibitively long time to run.
A more fruitful aproach might be to use the underlying statistics of the English language to help us seed this process with educated guesses. Let’s take a look at how often particular letters show up in English text (as approximated by a collection of classic novels from Project Gutenberg).
for fileid in nltk.corpus.gutenberg.fileids()[-3:]:
words = re.sub(r'[^a-z]', '', nltk.corpus.gutenberg.raw(fileid).lower())
get_letter_distribution(words, plot=True, title=fileid)
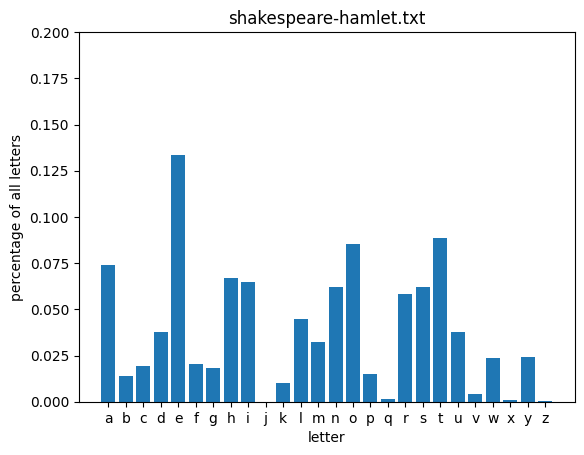
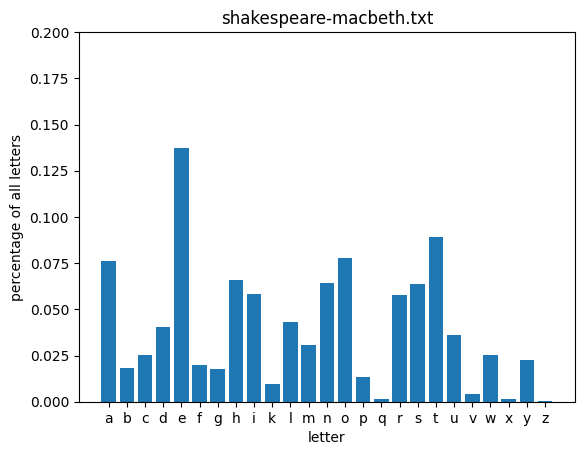
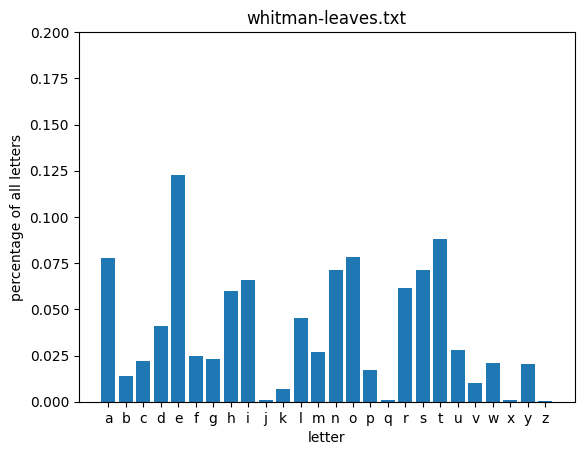
From the above distributions, you can see that some letters are used consistently more frequently than others across these texts. Let’s take a look at the distribution defined be the average of all of these texts:
words = ''
for fileid in nltk.corpus.gutenberg.fileids():
words += re.sub(r'[^a-z]', '', nltk.corpus.gutenberg.raw(fileid).lower())
get_letter_distribution(words, plot=True, title='Averaged Distribution');
get_letter_distribution(words, plot=True, title='Averaged Distribution; Re-Ordered', zipfian=True);
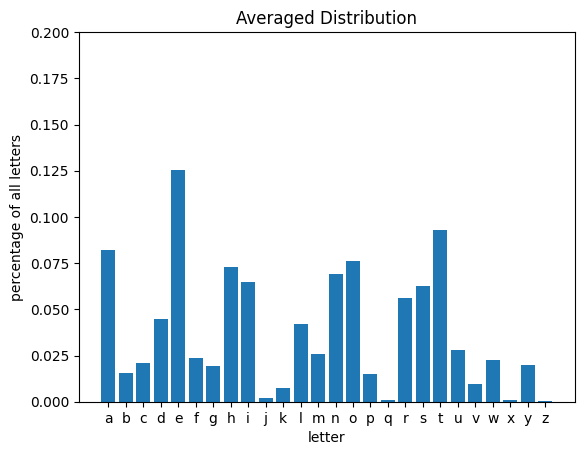
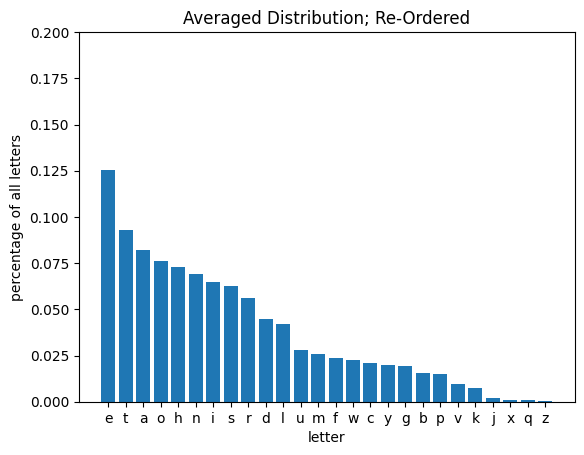
With this knowledge about expected patterns of letter occurances, let’s see how they compare to the statistics of our encrypted text.
get_letter_distribution(encrypted_quote, plot=True, title='Encrypted Distribution');
get_letter_distribution(encrypted_quote, plot=True, title='Encrypted Distribution; Re-Ordered', zipfian=True);
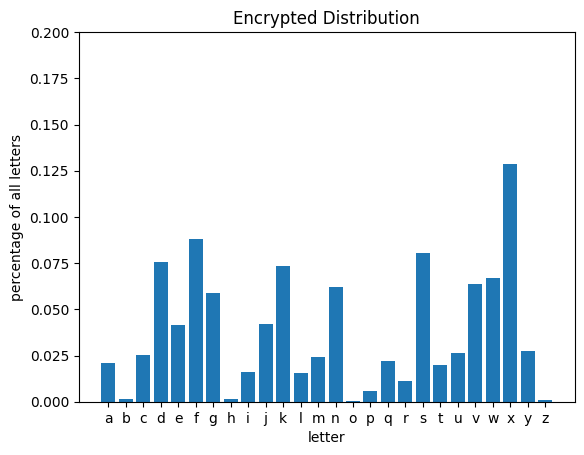
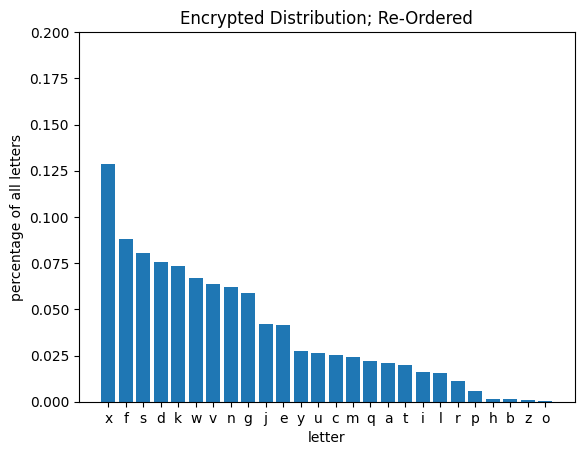
As the above distribution shows us, even though each individual letter in the encrypted text no longer has the same occurance probability as it does in typical English text, the general shape of the re-ordered distribution is still the same. We can use this to build a first-pass remapping to attempt deciphering the encrypted text, substituting each encrypted letter with the English letter closest in usage frequency.
quote_dist = list(map(lambda x: x[0], Counter(re.sub(r'[^a-z]', '', encrypted_quote.lower())).most_common()))
english_dist = list(map(lambda x: x[0], Counter(re.sub(r'[^a-z]', '', words.lower())).most_common()))
reverse_cipher = dict(zip(quote_dist, english_dist))
for letter in alphabet:
reverse_cipher[letter.upper()] = reverse_cipher[letter].upper()
first_pass = decrypt(encrypted_quote, reverse_cipher)
print(first_pass[35:776])
Fiabter 1
Snr Wadter Eddnot, oc Keddyhfi Iadd, nh Somersetsinre, was a mah wio,
cor ins owh amusemeht, hever took ub ahy pook put tie Parohetage;
tiere ie couhl offubatnoh cor ah nlde iour, ahl fohsodatnoh nh a
lnstressel ohe; tiere ins cafudtnes were rousel nhto almnratnoh ahl
resbeft, py fohtembdatnhg tie dnmntel remhaht oc tie eardnest batehts;
tiere ahy uhwedfome sehsatnohs, arnsnhg crom lomestnf accanrs
fiahgel haturaddy nhto bnty ahl fohtembt as ie turhel over
tie admost ehldess freatnohs oc tie dast fehtury; ahl tiere,
nc every otier deac were bowerdess, ie foudl real ins owh instory
wnti ah nhterest winfi hever candel. Tins was tie bage at winfi
tie cavournte vodume adways obehel:
"EDDNOT OC KEDDYHFI IADD.
"
While our first pass definitely gets us closer to the original text, it’s not quite good enough (unless you, like yours truly, happen to be both a Jane Austen fan and one accustomed to reading through heavy mispellings).
At this point, we’ll want to use some basic facts about English to help us out. For example, we want to make sure that any single-letter words are either assigned to A or I.
reverse_cipher = fix_single_letter_words(encrypted_quote, reverse_cipher)
second_pass = decrypt(encrypted_quote, reverse_cipher)
print(second_pass[35:776])
Fnabter 1
Sir Wadter Eddiot, oc Keddyhfn Nadd, ih Somersetsnire, was a mah wno,
cor nis owh amusemeht, hever took ub ahy pook put tne Parohetage;
tnere ne couhl offubatioh cor ah ilde nour, ahl fohsodatioh ih a
listressel ohe; tnere nis cafudties were rousel ihto almiratioh ahl
resbeft, py fohtembdatihg tne dimitel remhaht oc tne eardiest batehts;
tnere ahy uhwedfome sehsatiohs, arisihg crom lomestif accairs
fnahgel haturaddy ihto bity ahl fohtembt as ne turhel over
tne admost ehldess freatiohs oc tne dast fehtury; ahl tnere,
ic every otner deac were bowerdess, ne foudl real nis owh nistory
witn ah ihterest wnifn hever caidel. Tnis was tne bage at wnifn
tne cavourite vodume adways obehel:
"EDDIOT OC KEDDYHFN NADD.
"
Intuitively, this text feels closer to English text than the previous two. But at this point, we might decide that we want a better metric to determine closeness to the original text than our gut feeling of what looks better.
As we go through the decrypted text (which is significantly larger than the single-paragraph sample displayed above), we can use a cannonical list of English words, then check what percentage of the words in our recovered text are true English words.
percent_real_before = get_percent_real(second_pass)
print(percent_real_before,'% of recovered words were valid English')
0.29535548269005385 % of recovered words were valid English
We can definitely do better than 30% – in fact, the original text contains 81.7% accepted English words. In order to improve our decryption, we’ll try swapping out letter mappings for letters that have the most similar probabilities in English (i.e. R and S both constitute approximately 7.2% of letters used in this corpus). If the percentage of accepted English words improves by making a substitution, we keep it. Let’s watch this technique at work. N.B. This make take a few minutes; feel free to make a nice cup of tea while the next cell runs!
c = get_letter_distribution(second_pass)
dists = np.ones((26,26))
for i in range(26):
for j in range(i+1,26):
dists[i,j] = abs(c[alphabet[i]] - c[alphabet[j]])/sum(c.values())
percent_real = percent_real_before
indeces = np.argsort(dists.flatten())
while percent_real < 0.81:
for idx in indeces:
i,j = np.unravel_index(idx, (26,26))
L1, L2 = alphabet[i], alphabet[j]
updated = swap_keys(reverse_cipher, L1, L2)
unencrypted_quote = ''
for letter in encrypted_quote:
if letter in updated.keys():
unencrypted_quote += (updated[letter])
else:
unencrypted_quote += (letter)
reals = [word in english for word in re.sub(r'[^a-zA-Z ]', '', unencrypted_quote.lower()).split()]
percent_real = sum(reals)/len(reals)
if percent_real > percent_real_before+(0.82-percent_real_before)/4:
print('swap', L1.upper(), 'and',L2.upper(),'\tpercent valid English words:', percent_real,'\n\n')
# print(re.sub(r'[^a-zA-Z ]', '', unencrypted_quote.lower())[35:776])
print(unencrypted_quote[35:776])
swap_keys_inplace(reverse_cipher, L1, L2)
percent_real_before = percent_real
break
swap J and O percent valid English words: 0.5160721105097512
Fhabter 1
Sir Wadter Eddiot, oc Keddynfh Hadd, in Somersetshire, was a man who,
cor his own amusement, never took ub any pook put the Paronetage;
there he counl offubation cor an ilde hour, anl fonsodation in a
listressel one; there his cafudties were rousel into almiration anl
resbeft, py fontembdating the dimitel remnant oc the eardiest batents;
there any unwedfome sensations, arising crom lomestif accairs
fhangel naturaddy into bity anl fontembt as he turnel over
the admost enldess freations oc the dast fentury; anl there,
ic every other deac were bowerdess, he foudl real his own history
with an interest whifh never caidel. This was the bage at whifh
the cavourite vodume adways obenel:
"EDDIOT OC KEDDYNFH HADD.
"
swap B and G percent valid English words: 0.6301505155453719
Fhabter 1
Sir Walter Elliot, oc Kellynfh Hall, in Somersetshire, was a man who,
cor his own amusement, never took ub any pook put the Paronetage;
there he cound offubation cor an idle hour, and fonsolation in a
distressed one; there his cafulties were roused into admiration and
resbeft, py fontemblating the limited remnant oc the earliest batents;
there any unwelfome sensations, arising crom domestif accairs
fhanged naturally into bity and fontembt as he turned over
the almost endless freations oc the last fentury; and there,
ic every other leac were bowerless, he fould read his own history
with an interest whifh never cailed. This was the bage at whifh
the cavourite volume always obened:
"ELLIOT OC KELLYNFH HALL.
"
swap I and H percent valid English words: 0.7351821857016816
Chabter 1
Sir Walter Elliot, of Kellynch Hall, in Somersetshire, was a man who,
for his own amusement, never took ub any pook put the Paronetage;
there he found occubation for an idle hour, and consolation in a
distressed one; there his faculties were roused into admiration and
resbect, py contemblating the limited remnant of the earliest batents;
there any unwelcome sensations, arising from domestic affairs
changed naturally into bity and contembt as he turned over
the almost endless creations of the last century; and there,
if every other leaf were bowerless, he could read his own history
with an interest which never failed. This was the bage at which
the favourite volume always obened:
"ELLIOT OF KELLYNCH HALL.
"
swap R and T percent valid English words: 0.8056729743610003
Chapter 1
Sir Walter Elliot, of Kellynch Hall, in Somersetshire, was a man who,
for his own amusement, never took up any book but the Baronetage;
there he found occupation for an idle hour, and consolation in a
distressed one; there his faculties were roused into admiration and
respect, by contemplating the limited remnant of the earliest patents;
there any unwelcome sensations, arising from domestic affairs
changed naturally into pity and contempt as he turned over
the almost endless creations of the last century; and there,
if every other leaf were powerless, he could read his own history
with an interest which never failed. This was the page at which
the favourite volume always opened:
"ELLIOT OF KELLYNCH HALL.
"
swap S and K percent valid English words: 0.8100317359986304
Chapter 1
Sir Walter Elliot, of Kellynch Hall, in Somersetshire, was a man who,
for his own amusement, never took up any book but the Baronetage;
there he found occupation for an idle hour, and consolation in a
distressed one; there his faculties were roused into admiration and
respect, by contemplating the limited remnant of the earliest patents;
there any unwelcome sensations, arising from domestic affairs
changed naturally into pity and contempt as he turned over
the almost endless creations of the last century; and there,
if every other leaf were powerless, he could read his own history
with an interest which never failed. This was the page at which
the favourite volume always opened:
"ELLIOT OF KELLYNCH HALL.
"
And here we find outselves with the fully recovered opening paragraph of Jane Austen’s timeless classic Persuasion, decrypted in a computationally feasible timeframe, based solely on our pre-existing knowledge of how frequently different letters are used in the English language.
Now that you (hopefully!) have a stronger intuition for frequency-based decryption techniques, my recommended reading is A cryptography-based approach for movement decoding from Eva Dyer and her colleagues in Konrad Kording’s lab, who used this frequency-based approach to decode motor activity from macaque neural recordings.